refacare.blogg.se - Non linear scatter plot

Therefore, it may be tempting to always choose an equation of the higher order. In most cases, higher order equations seem to fit all points of the past data better than a lower order equation. As we increase the order (to a maximum of 6), we can see how the curve changes. When we select a “Polynomial” trendline, Excel starts with an equation of order 2. The choice between linear and nonlinear models for a given dataset is a tradeoff between the fit of the model (which impacts the accuracy of the forecast made from the model), and the complexity of the model building and calculation. If a nonlinear model significantly improves the fit over a linear model, it would good to use the nonlinear model. After that, you may want to build a nonlinear model on the same data and check the fit to see if it improves. In general, it is better to always start with a linear model and then checking the fit of the model. Therefore, it is important to understand that there are no rules regarding linear and nonlinear models. That linear model would have been a valid model as well. We could have created a linear model for the above data.

What is a suitable order to use for a nonlinear model?.

Two questions might immediately arise at this point: We now have our order 3 nonlinear regression model for the data, y = 0.783x 3 – 50.113x 2 + 1043.1x – 6830.4. Let us look at an order 3 equation for our data. As we change the order of the equation we can see the trend line change. As soon as we select “Polynomial”, the “Order” field next to it is enabled and we can set the order of the desired equation.Įxcel allows us to choose an equation of order 2 to order 6. We will select “Polynomial” (poly = many, nominal = names refers to different x terms) trendline to get the nonlinear equation that we are looking for. The default trendline is linear, however, the trendline dialog box has the option to add other trendiness. Next, we will add a trendline on the above data. Take a look at the following data that lists out some motorbike models, their mileage (in kilometres per litre), and their dry weight (in kilograms): Similar to how we built a linear regression model on Excel using a scatter plot, we will build a nonlinear regression model. Identifying the nonlinear regression model For example, y = ax 4 + cx 2 + dx + e simply means, that the coefficient of x 3 is zero, and the term is, therefore, omitted. In such cases, that term is simply omitted while writing the equation.

It is important to note here that the coefficients of some x terms may be zero. The highest power that x is raised to in this equation is 4, and therefore this is a degree (or order) 4 equation.ĭid you notice that the power to which x is raised to, always reduces by 1 for each consecutive x term? Since this not an equation of order 1, it is a nonlinear equation.Īnother nonlinear equation could be of the form y = ax 4 + bx 3 + cx 2 + dx + e.

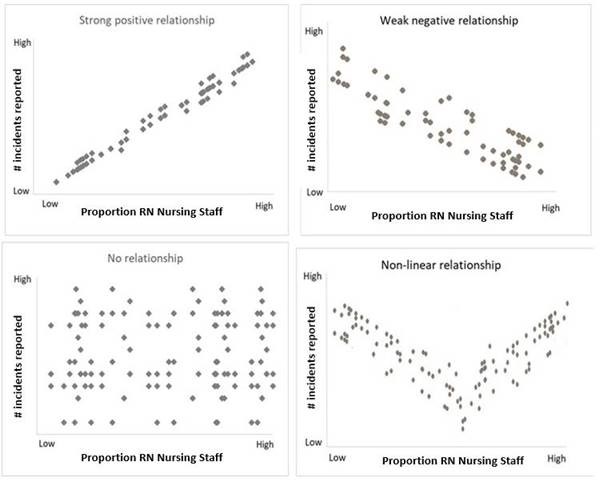
For example, the equation y = ax 2 + bx + c has one term with x raised to the power 2, and therefore, the degree (or order) of the equation is 2. This is what we refer to when we say that the degree (also called the order) of the equation is 1.Ī nonlinear equation would have a degree not equal to 1. The variable x in this equation is raised to the power of 1. Linear equations have a degree equal to 1.Ī linear equation is of the form, y = ax + b. Nonlinear equations have a degree either less than 1, or greater than 1 (but never a degree equal to 1). How are nonlinear equations different from linear equations? The simple answer is that in a linear equation, the change in the dependent variable is always proportional to the change in the independent variable however, in a nonlinear equation, the dependent variable changes disproportionately with a change in the independent variable. Naturally, the equation of the model is a nonlinear equation. A nonlinear regression model is one that describes a nonlinear relationship between the dependent and the independent variables. We have talked about regression models in the context of linear regression models in the previous post.